PoPL Lecture 9

Revision

• Inductive term cannot be a subterm of itself, but a coinductive term can be.

Bisimulation

• A quick flashback to term graphs and behaviours \(\sigma\)

  

• A motivation for bisimulation: all the terms are intuitively the same

  

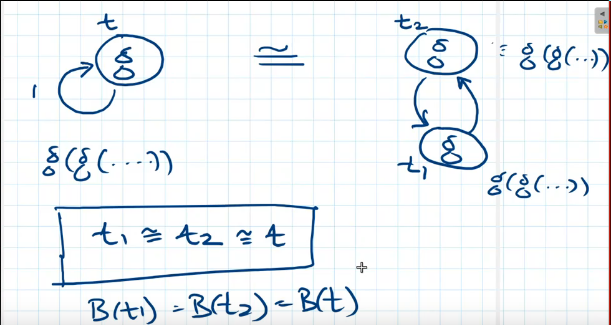
• Bisimilarity establishes equivalence of behavious by examining the structure of the term graph containing two vertices:
  • Equivalence of objects is modulo observation
  • In case of terms, observations are constructor symbols and we are allowed to look at the head of the term in order to identify the constructor
  • Equal terms should have equal heads + equality for corresponding pair of subterms –> Inference rule down, and rule up
  • Issues with circular reasoning, however
  • Intuitive idea behind bisimulation: just say that the 2 things are equal, and challenge anyone to show a mistake.
  • Unlike induction, here you construct an argument and then ask people to pick holes in it. Proof by construction, where it is entirely internally consistent.
• So, for bisimilarity R:
  • hd(v) == hd(v')
  • for each i, \(1 \leq i \leq \alpha (hd(v))\), for all i: $subterm_i(v), subterm_i(v’) \in R$

• Non-example

  

• Setup for a bisimilarity proof

  

  Demonstration of showing/proof:

  

• Setup for a bisimulation break

  

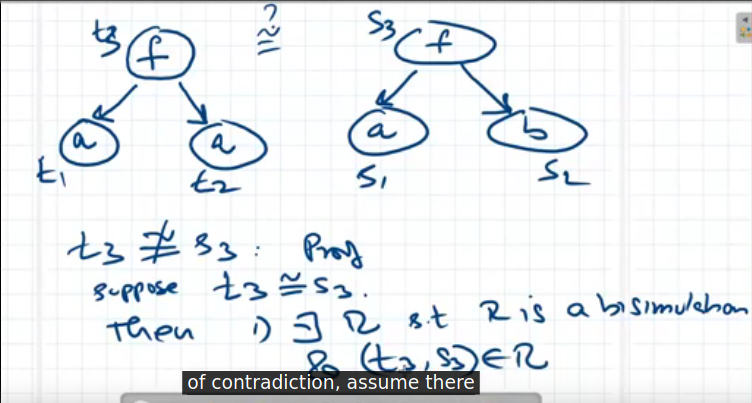
  Proof:

Replacement for inductive terms

• Replace subterm t' at position p, with say S

Replacement for coinductive terms